Processingで歯車（その2 噛み合い編）

はじめに

前回は歯車の作成をしました。そこで今回は、2つの歯車を使って回転、噛み合わせをやっていこうと思います。

歯車の作成は以下を参考にしてください。

歯数とモジュールを決める

前回同様、歯車を作成するために歯数とモジュールを最初に決定します。

ここで大きい歯車（駆動歯車）の歯数\(z_1\)を24、小さい歯車（被動歯車）の歯数\(z_2\)を12とします。

ここで重要なのが、歯車を噛み合わせるためにはモジュールを等しくしなければなりません。

なので、2つの歯車のモジュールを今回は10と設定します。

歯車対の中心距離

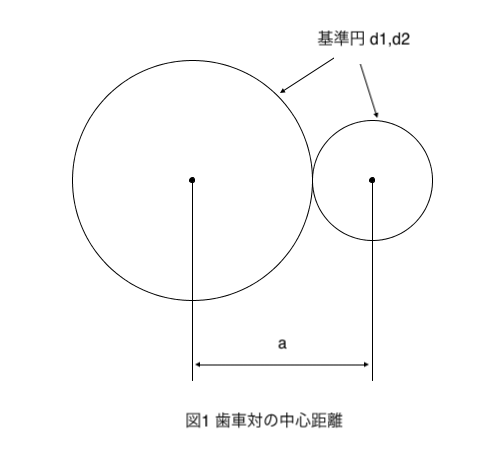
歯車の中心距離aは、駆動歯車と被動歯車の基準円直径を\(d_1\),\(d_2\)とすると以下の式で求められます。

\[a=\frac{d_1+d_2}{2}=\frac{m(z_1+z_2)}{2}\]

ここで前回説明したように後半の式は、基準円直径はモジュールと歯数をかけても求められるのでこうなりました。

歯車2つの速度伝達比

速度伝達比\(i\)は、駆動歯車の角速度\(\omega_1\)を被動歯車の角速度\(\omega_2\)で除した値として定義されるので以下の式になります。

\[i=\frac{\omega_1}{\omega_2}\]

次に、基準円直径とモジュール、歯数の関係式(両歯車のモジュールが等しい)。および、基準円上の周速度が両歯車で等しいという条件から以下の式の関係が得られます。

\[m=\frac{d_1}{z_1}=\frac{d_2}{z_2}\]

\[v = \frac{d_1\omega_1}{2}=\frac{d_2\omega_2}{2}\]

よって速度伝達比\(i\)は、

\[i=\frac{\omega_1}{\omega_2}=\frac{d_2}{d_1}=\frac{z_2}{z_1}\]

以上の式で、歯車の周速度は歯数の比で求められました。

また、歯車2つの時は、駆動歯車と被動歯車の回転方向は逆になりますのでコードを書く時は気をつけましょう。

アニメーション

以上をコードに組み込めば、歯車の噛み合いのアニメーションができます。

Processingで2つの歯車の噛み合い #Processing
2つの歯車では互いの回転方向が逆になる
歯数の比で速度伝達比が決まる。 pic.twitter.com/7WaunJZK55
— かめのの (@kameno_no3) November 26, 2020

Processingで2つの歯車の噛み合い

以下が2つの歯車の噛み合いのコードです。クラスと配列を利用しています。

Gear[] gears = new Gear[2];
color bg = #D8EFFC; //背景色
color c0 = #004EA2; //駆動歯車の色
color c1 = #E8352B; //被動歯車の色

void setup() {
  size(700, 600);
  gears[0] = new Gear(PI/9, 24, 10, c0); //圧力角PI/9(20°), 歯数:z=24, モジュール:m=18
  gears[1] = new Gear(PI/9, 12, 10, c1); //圧力角PI/9(20°), 歯数:z=12, モジュール:m=18
}

void draw() {
  background(bg);
  //駆動歯車の位置、y座標は同じ
  float x0 = 250;
  float y = 250;
  //被動歯車の位置
  float x1 = (gears[0].d+gears[1].d)/2;
  //被動歯車の速度計算
  float i = gears[0].z / gears[1].z;
  
  float omega = PI/300;
  gears[0].move(x0, y, omega);
  gears[1].move(x0+x1, y, -i * omega); 
}

class Gear {
  float d, r, ra, rb, rf;
  float alpha, z, m;
  color col;
  float angle = 0;
  //インボリュート関数
  float inv(float a) { 
    return tan(a) - a;
  }

  Gear(float _alpha, float _z, float _m, color col_) {
    alpha = _alpha;
    z = _z;
    m = _m;
    d = m * z;
    r = (m * z)/2; //基準円半径
    ra = ((z+2) * m)/2; //歯先円半径
    rb = (d * cos(alpha))/2; //基礎円半径
    rf = ((z-2.5) * m)/2; //歯底円半径
    col = col_;
  }

  void display() {
    float beta = acos(rb/ra);
    float x2 = ra*cos(inv(beta));
    float phi_2 = acos(x2/ra); //点2の角度

    float theta_b = PI/z + 2*(inv(alpha));
    float x3 = ra*cos(inv(beta) - theta_b);
    float phi_3 = acos(x3/ra); //点3の角度

    float x5 = rf*cos(theta_b);
    float y5 = rf*sin(theta_b);
    
    fill(col);
    beginShape();
    for (float j = 0; j < 2*PI; j+=2*PI/z) {
      //歯元部
      vertex(rf*cos(j), -rf*sin(j));
      vertex(rb*cos(j), -rb*sin(j));

      //基礎円から歯先円までのインボリュート曲線
      for (float r = rb; r <= ra; r+=0.5) {
        float beta_r = acos(rb/r);
        float x12 = r*cos(inv(beta_r));
        float y12 = r*sin(inv(beta_r));
        float x12j = x12*cos(j) - y12*sin(j);
        float y12j = x12*sin(j) + y12*cos(j);
        vertex(x12j, -y12j);
      }

      //歯先円
      for (float i = phi_2; i <= phi_3; i+=0.03f) {
        float x23 = ra*cos(i);
        float y23 = ra*sin(i);
        float x23j = x23*cos(j) - y23*sin(j);
        float y23j = x23*sin(j) + y23*cos(j);
        vertex(x23j, - y23j);
      }

      //反転のインボリュート曲線
      for (float r = ra; r >= 0; r-=0.5) {
        float beta_r = acos(rb/r);
        float x34 = r*cos(inv(beta_r) - theta_b);
        float y34 = r*sin(inv(beta_r) - theta_b);
        float x34j = x34*cos(-j) - y34*sin(-j);
        float y34j = x34*sin(-j) + y34*cos(-j);
        vertex(x34j, y34j);
      }

      //点4から点5の線
      vertex(x5*cos(j)-y5*sin(j), -x5*sin(j)-y5*cos(j));

      //歯底円
      for (float i = theta_b; i <= 2*PI/z; i+=0.03f) {
        float x56 = rf*cos(i);
        float y56 = rf*sin(i);
        float x56j = x56*cos(j) - y56*sin(j);
        float y56j = x56*sin(j) + y56*cos(j);
        vertex(x56j, -y56j);
      }
    }
    endShape();
  }

  //穴の作成
  void hole() {
    noStroke();
    fill(bg);
    ellipse(0, 0, r/3, r/3);
  }

  //歯車の回転
  void move(float x_, float y_, float omega_) {
    float x = x_;
    float y = y_;
    float omega = omega_;
    pushMatrix();
    translate(x, y);
    rotate(angle);
    display();
    hole();
    popMatrix();
    angle += omega;
  }
}