はじめに
Processingで歯車を作成し、回転までさせてみようと思います。歯車にも種類がありますが、今回は転位なしの標準平歯車を作成します。
また、歯型の作成にサイクロイド曲線を用いるサイクロイド歯車と、インボリュート曲線を用いるインボリュート歯車がありますが、インボリュート歯車を作成したいと思います。
いろいろ調べながら作成しましたが、間違っている可能性もあるためその際はご教示いただけたら幸いです
モジュール、歯数、圧力角を決める
歯車を作るにあたり、以下の3つが必要です。
- m : モジュール(歯のサイズ)
- z : 歯の数
- α : 圧力角
今回は、m = 18 , z = 15 , α = 20°と決めて歯車を作りたいと思います。
4つの円
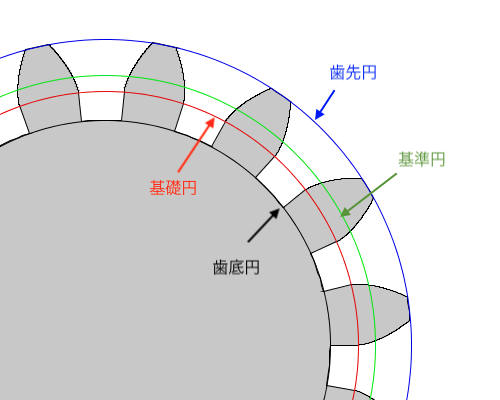
モジュール、歯数、圧力角を決めると、以下の4つの円を描けることができます。
- 歯先円 \(d_a\) : 歯の先端を通る仮想の円
- 基準円 \(d\) : 摩擦車の外周円に相当する仮想の円
- 基礎円 \(d_b\) : インボリュート曲線の基礎となる仮想の円
- 歯底円 \(d_f\) : 歯元を通る仮想の円
この4つの円の直径は、モジュール、歯数、圧力角が決まっていると以下の式より求められます。

また、実際に使うのは直径ではなく半径なので以下の文では、\(r\)に添え字で表していきます。
歯車の描き方の手順
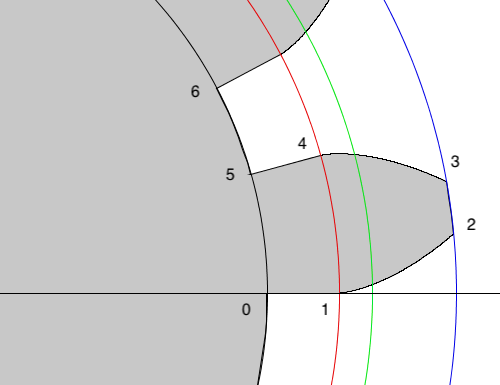
まずは点0の座標を\((r_f,0)\)とした1つの歯型を描きたいと思います。
Processingでvertexで描くので0〜6までの座標を求めます。以下は1つの歯型を描く考え方です。
- 0→1、4→5 : 基礎円から歯車の中心まで線を描く。
- 1→2 : 基礎円からインボリュート曲線で歯先円まで描く。
- 2→3 : 歯先円。
- 3→4 : インボリュート曲線を反転させて描く。
- 5→6 : 歯底円。
それでは、各座標を求めてみましょう。
0→1 : 基礎円から歯車の中心までの線
ここは単純に点0と点1のy座標が0なので、
点0の座標は、\((r_f,0)\,\),点1の座標は、\((r_b,0)\)となります。
点0と点1の座標をvertexで繋げましょう。
float x0 = rf;
float x1 = rb;
vertex(x0, 0);
vertex(x1, 0);ちなみに、最終のコードは最後に載せるのでここでは参考程度にしてください。
1→2 : インボリュート曲線で片側の歯型を描く
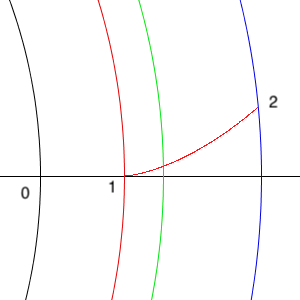
インボリュート曲線については前回書いてみたので以下を参考にしてください。
ここでインボリュート関数を用いた以下の式を使います。
\begin{eqnarray*}
\beta & = & cos^{-1}\frac{r_b}{r} \\
inv\,\beta& = & \tan\beta-\beta \\
x & = & r\cos(inv\,\beta) \\
y & = & r\sin(inv\,\beta) \\
\end{eqnarray*}
ここで、\(r\)は歯車の中心からの距離を表します。インボリュート曲線は、基礎円から歯先円まで描くので、\(r\)を基礎円半径\(r_b\)から歯先円半径\(r_a\)まで増加させます。
以上のことをfor文を使って以下のように書きます。
//インボリュート関数の定義
float inv(float a) {
return tan(a) - a;
}
//基礎円半径rbから歯先円半径raまでインボリュート曲線を描く
for (float r = rb; r < ra; r+=0.1) {
float beta = acos(rb/r);
float x12 = r * cos(inv(beta));
float y12 = r * sin(inv(beta));
vertex(x12, -y12);
}3→4 : インボリュート曲線を反転させて反対側の歯型を描く
点3の座標を得るために先に3→4の説明をします。
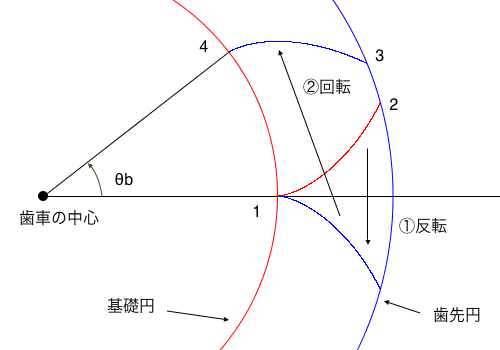
まず、先程のインボリュート曲線を反転させます。
Processingではy座標を+にすればいいです。
反転させたら、\(\theta_b\)回転させます。
\(\theta_b\)の値については、以下の記事が非常に参考になりました。(\(\theta_b\)の値だけでなく今回の記事全般的に参考になりました。)

記事によると\(\theta_b\)の値は、以下のようになります。
\[\theta_b=\frac{\pi}{z}+2inv\,\alpha\]
ここでのインボリュート関数\(inv\,\alpha\)の角度\(\alpha\)は圧力角なので20°になります。
コードは以下のように書きます。
//歯先円半径raから基礎円半径rbまで反転させたインボリュート曲線を描く
for (float r = ra; r>=rb; r-=0.1) {
float alpha = PI/9; //圧力角20°はPI/9
float beta_r = acos(rb/r);
float theta_b = PI/z + 2*(inv(alpha));
float x34 = r*cos(inv(beta_r)-theta_b);
float y34 = r*sin(inv(beta_r)-theta_b);
vertex(x34,y34);
}2→3 : 歯先を描く
点2と点3の座標が求まったので、歯先をvertexで描きましょう
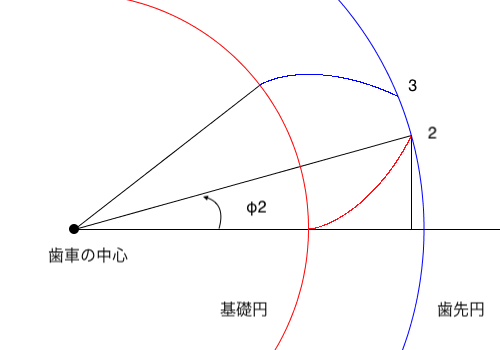
円を描くので角度を求めます。
ここで点2のx座標は、\(\beta=\cos^{-1}\displaystyle\frac{rb}{ra}\,\)なので、インボリュート曲線の式より、
\[x_2=ra\cos(inv\,\beta)\]
図の斜辺は歯先円半径なので\(r_a\,\)となるので、余弦定理より角度\(\phi_2\)は
\[\phi_2=\cos^{-1}\frac{x_2}{r_a}\]
同様に考え、点3の角度\(\phi_3\)は
\[\phi_3=\cos^{-1}\frac{x_3}{r_a}\]
以上のことをfor文を使って書きましょう。
//角度φ2を求める
float beta = acos(rb/ra);
float x2 = ra*cos(inv(beta));
float phi_2 = acos(x2/ra);
//角度φ3を求める
float theta_b = PI/z + 2*(inv(alpha));
float x3 = ra*cos(inb(beta) - theta_b);
float phi_3 = acos(x3/ra);
//φ2からφ3まで円を描く
for (float i = phi_2; i <= phi_3; i+=0.03f) {
float x23 = ra*cos(i);
float y23 = ra*sin(i);
vertex(x23,-y23);
}4→5 : 点4から歯車の中心までの線
点4と点5の座標はそれぞれ以下のようになります。
\begin{eqnarray*}
(x_4\,,y_4) =(r_b\cos\theta_b\,,r_b\sin\theta_b) \\
(x_5\,,y_5) = (r_f\cos\theta_b\,,r_f\sin\theta_b) \\
\end{eqnarray*}
コードは以下のように書きます。
//点4の座標
float x4 = rb*cos(theta_b);
float y4 = rb*sin(theta_b);
//点5の座標
float x5 = rf*cos(theta_b);
float y5 = rf*sin(theta_b);
//点4から点5の線
line(x4, y4, x5, y5);5→6 : 歯底円を描く
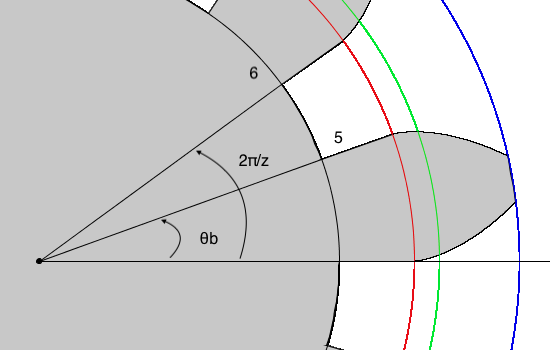
歯先円のときと同様に点5と点6が求められているので、歯底円をvertexで描きます。
点5の角度は、\(\theta_b\)となり、点6の角度は2π/zとなります。
点6の角度の考え方は、歯1つあたりの角度が2π/zだからです。
これで歯型が作れたのでコピーを作成します
作った歯型を歯数の分だけ回転してコピーを作成する
回転座標の式は以下のようになります。
\begin{eqnarray*}
x_j & = & x\cos\frac{2\pi j}{z}-y\sin\frac{2\pi j}{z} \\
y_j & = & x\sin\frac{2\pi j}{z}+y\cos\frac{2\pi j}{z} \\
\end{eqnarray*}
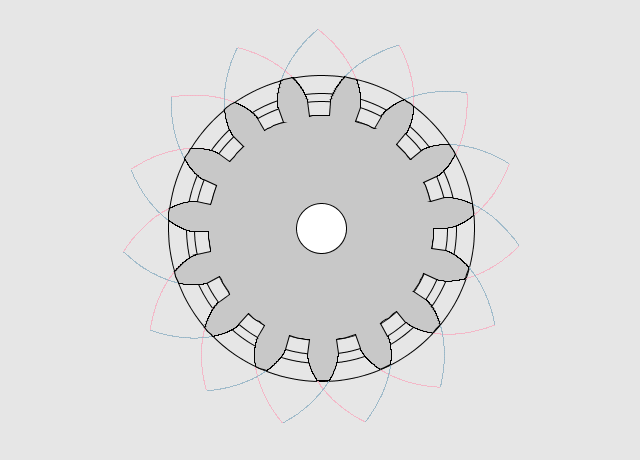
これで色を付けて、お好みで穴を開ければ歯車は完成です。
コードは長くなってしまったので2ページ目に書いたので参考にしてください。
アニメーション
インボリュート歯車の描き方の動画を作ってみたので参考にしてください。


コメント