Processingで外サイクロイド・トロコイド曲線を作る

はじめに
外サイクロイド・トロコイド曲線とは？
1. 点P\((x,y)\)の位置を求める
2. 外サイクロイド・トロコイド曲線の山の数
Processingで外サイクロイド・トロコイド曲線
1. アニメーション
おまけ：カージオイド曲線
参考文献
関連記事

はじめに

前回は、直線サイクロイド・トロコイド曲線をProcessingで作ったので、今回は外サイクロイド・トロコイド曲線を作りたいと思います。

外サイクロイド・トロコイド曲線とは？

定円の外側を動円が転がるとき、動円の円周上の点が描く軌跡を外サイクロイドまたはエピサイクロイドといい。

また、動円の内部または外部の点が描く軌跡を外トロコイドまたはエピトロコイドといいます。

Processingで動かすために動円上の点、内部または外部の点 P(x,y)の求め方を見ていきましょう。

点P\((x,y)\)の位置を求める

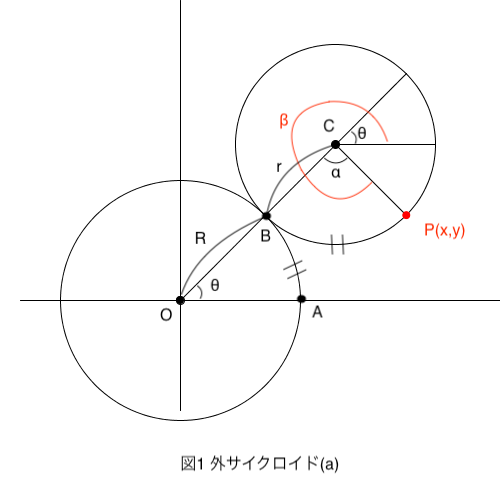
2円の接点をBとし、\(\angle\)BCP=αとします。\(\stackrel{\frown}{PB}\)=\(\stackrel{\frown}{AB}\) より、

\[r\cdot\alpha=R\cdot\theta　\rightarrow　\alpha=\displaystyle\frac{R}{r}\theta\]

\(\vec{CP}\)の\(x\)軸の正方向からの回転角βは

\[\beta=\pi+\theta+\alpha=\pi+\displaystyle\frac{r+R}{r}\theta\]

\(\vec{CP}=(r\cos\beta,r\sin\beta)\)　になり、
\(\cos(\pi+\theta)=-\cos\theta\,,\sin(\pi+\theta)=-\sin\theta\)　なので　\(\vec{CP}\)　は

\begin{eqnarray*}
\vec{CP} & = & (r\cos(\pi+\displaystyle\frac{r+R}{r}\theta),\,r\sin(\pi+\displaystyle\frac{r+R}{r}\theta)) \\
& = & (-r\cos\displaystyle\frac{r+R}{r}\theta,\,-r\sin\displaystyle\frac{r+R}{r}\theta) \end{eqnarray*}

\(\vec{OP}=\vec{OC}+\vec{CP}\)　より　\(\vec{OP}\)　は

\[\vec{OP}=\left((r+R)\cos\theta-r\cos\displaystyle\frac{r+R}{r}\theta,\,(r+R)\sin\theta-r\sin\displaystyle\frac{r+R}{r}\theta\right)\]

よって、点Pのx座標、y座標は以下になります。

\begin{cases}
x=(R+r)\cos\theta-r\cos\displaystyle\frac{(R+r)\theta}{r} \\
y=(R+r)\sin\theta-r\sin\displaystyle\frac{(R+r)\theta}{r}
\end{cases}

また、動円の内部、外部の点の長さを\(l\)だとすると、\(\vec{CP}\)の式の\(r\)を\(l\)と置き換えることで動円の内部、外部の軌道を表現できます。

外サイクロイド・トロコイド曲線の山の数

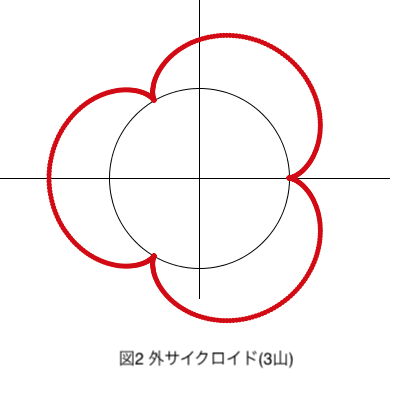
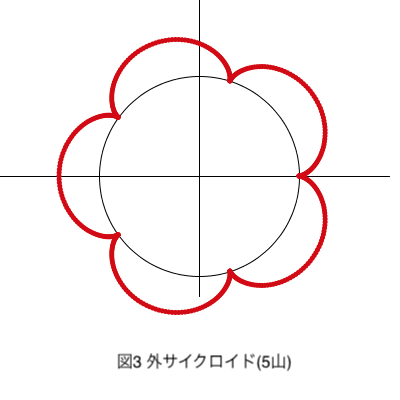
上図は外サイクロイド曲線です。

定円の半径をR、動円の半径をrとすると、山の数nは\(\displaystyle\frac{R}{r}\)となります。

図2はR = 90 , r = 30 より3山、図3はR = 100 , r = 50 で5山です。

Processingで外サイクロイド・トロコイド曲線

以下がProcessingで外サイクロイド・トロコイド曲線を動かすコードになります。
前回同様に理解しやすくするためにボタンも実装してみました。

PGraphics pg1, pg2, pg3;
float x, y;
float rad = 0;
float R = 90; //定円半径
float r = 30; //動円半径

boolean Cyc1 = false;
boolean Cyc2 = false;
boolean Cyc3 = false;
boolean roll = false;
boolean show1 = false;
boolean show2 = false;
boolean show3 = false;

void setup() {
  size(400, 400);
  pg1 = createGraphics(width, height);
  pg2 = createGraphics(width, height);
  pg3 = createGraphics(width, height);
}

void draw() {
  background(230);
  //定円
  noFill();
  ellipse(width/2, 180, R*2, R*2);
  Button();
  rad += 0.8;
  //ボタン操作
  if (Cyc1) Cycloid1(); //外サイクロイド(r=l)
  if (Cyc2) Cycloid2(15); //外トロコイド(r>l)
  if (Cyc3) Cycloid3(55); //(r<l)
  //keyを押したら画像表示
  if (show1) image(pg1, 0, 0);
  if (show2) image(pg2, 0, 0);
  if (show3) image(pg3, 0, 0);
}

void Button() {
  fill(255);
  rect(40, 350, 80, 30);
  rect(160, 350, 80, 30);
  rect(280, 350, 80, 30);
  fill(0);
  textSize(16);
  textAlign(CENTER, CENTER);
  text("r = l", 80, 365);
  text("r > l", 200, 365);
  text("r < l", 320, 365);
}
//動円
void Circle() {
  noFill();
  ellipse(width/2+(r+R)*cos(radians(rad)), 180-(r+R)*sin(radians(rad)), r*2, r*2);
}

void mouseClicked() {
  if (mouseX>=40 && mouseX<=120 && mouseY>=350 && mouseY<=380) {
    Cyc1 = !Cyc1;
    rad = 0;
  }
  if (mouseX>=160 && mouseX<=240 && mouseY>=350 && mouseY<=380) {
    Cyc2 = !Cyc2;
    rad = 0;
  }
  if (mouseX>=280 && mouseX<=360 && mouseY>=350 && mouseY<=380) {
    Cyc3 = !Cyc3;
    rad = 0;
  }
}

void keyPressed() {
  if (key == '1') {
    show1 = !show1;
    if (!show1) show1 = false;
  } else if (key == '2') {
    show2 = !show2;
    if (!show2) show2 = false;
  } else if (key == '3') {
    show3 = !show3;
    if (!show3) show3 = false;
  }
}

float rR = r + R;
void Cycloid1() {
  x = width/2 + rR*cos(radians(rad)) - r*cos(rR*radians(rad)/r);
  y = -180 + rR*sin(radians(rad)) - r*sin(rR*radians(rad)/r);
  Circle();
  pg1.beginDraw();
  pg1.noStroke();
  pg1.fill(209, 0, 0);
  pg1.ellipse(x, -y, 5, 5);
  pg1.endDraw();
  image(pg1, 0, 0);
  //円の中心とサイクロイド曲線上の点を結ぶ線分
  line(width/2+rR*cos(radians(rad)), 180-rR*sin(radians(rad)), x, -y);
  if (rad >= 360) {
    delay(3000); //1周したら3秒停止
    Cyc1 = !Cyc1;
  }
}

void Cycloid2(float l) {
  x = width/2 + rR*cos(radians(rad)) - l*cos(rR*radians(rad)/r);
  y = -180 + rR*sin(radians(rad)) - l*sin(rR*radians(rad)/r);
  Circle();
  pg2.beginDraw();
  pg2.noStroke();
  pg2.fill(0, 40, 205);
  pg2.ellipse(x, -y, 5, 5);
  pg2.endDraw();
  image(pg2, 0, 0);
  //円の中心とサイクロイド曲線上の点を結ぶ線分
  line(width/2+rR*cos(radians(rad)), 180-rR*sin(radians(rad)), x, -y);
  if (rad >= 360) {
    delay(3000);
    Cyc2 = !Cyc2;
  }
}

void Cycloid3(float l) {
  x = width/2 + rR*cos(radians(rad)) - l*cos(rR*radians(rad)/r);
  y = -180 + rR*sin(radians(rad)) - l*sin(rR*radians(rad)/r);
  Circle();
  pg3.beginDraw();
  pg3.noStroke();
  pg3.fill(74, 170, 64);
  pg3.ellipse(x, -y, 5, 5);
  pg3.endDraw();
  image(pg3, 0, 0);
  //円の中心とサイクロイド曲線上の点を結ぶ線分
  line(width/2+rR*cos(radians(rad)), 180-rR*sin(radians(rad)), x, -y);
  if (rad >= 360) {
    delay(3000);
    Cyc3 = !Cyc3;
  }
}