Processingでひし形タイリングその1

はじめに
1. ひし形タイリングの作り方
プログラム
参考文献
関連記事

はじめに

今回は「美しい幾何学」第19章の挿絵を参考にProcessingで作ります。

リンク

ひし形タイリングの作り方

正式な名前か分かりませんが、ひし形タイリングの作り方を解説します。

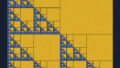
完成形は同一の立方体を積み重ねたように見えますが、図1の画像の正六角形をプログラムで作ってクラス化した後、上の層をずらして並べることで完成形の画像のようになります。ただし、一部は正六角形を重ねて書いてます。

図1の正六角形の作り方は、正六角形は6つの正三角形で作れることを利用し、図2のように左が黄色ひし形、真ん中が赤色ひし形、右が青色ひし形の正三角形を1つ作りそれを180度反転することで欲しい正三角形を6つ作ることができます。

プログラム

以下がひし形タイリングのプログラムです。上手くコードが書けなかったので長くなってしまいました。

PVector[] vec_y; //黄色ひし形の三角形
PVector[] vec_r; //赤ひし形の三角形
PVector[] vec_b; //青ひし形の三角形
ArrayList<Hex> hex = new ArrayList<Hex>();
float r = 80;

void setup() {
  size(500, 500);
  pixelDensity(2);
  vec_y = new PVector[3];
  vec_r = new PVector[3];
  vec_b = new PVector[3];
  
  //タイリング斜めに1回目
  for (int i = 0; i <=2; i++) {
    hex.add(new Hex(-i*r*cos(PI/6), i*r+i*r*sin(PI/6)));
  }
  //タイリング斜めに2回目
  hex.add(new Hex(r*cos(PI/6), r+r*sin(PI/6)));
  hex.add(new Hex(0, 2*r+2*r*sin(PI/6)));
  hex.add(new Hex(2*r*cos(PI/6), 2*r+2*r*sin(PI/6)));  
  //重なり左
  hex.add(new Hex(-r*cos(PI/6)-r/2*cos(PI/6), r/2+r/2*cos(PI/3)));
  hex.add(new Hex(-r*cos(PI/6)-r*cos(PI/6), r+r*cos(PI/3)));
  //重なり右
  hex.add(new Hex(r*cos(PI/6)+r/2*cos(PI/6), r/2+r/2*cos(PI/3)));
  hex.add(new Hex(r*cos(PI/6)+r*cos(PI/6), r+r*cos(PI/3)));
  //重なり下
  hex.add(new Hex(-r/2*cos(PI/6), 3*r+r/2+r/4));
  hex.add(new Hex(r/2*cos(PI/6), 3*r+r/2+r/4));
  noLoop();
}

void draw() {
  background(getCol3());
  powder();
  translate(width/2, 100);
  for (Hex hex : hex) {
    hex.display();
  }
}

void powder() {
  for (int i = 0; i < 500000; i++) {
    stroke(random(100,255), 60);
    strokeWeight(0.4);
    point(random(width), random(height));
  }
}

class Hex {
  float p_x, p_y;

  Hex(float p_x, float p_y) {
    this.p_x = p_x;
    this.p_y = p_y;
  }

  void display() {
    pushMatrix();
    translate(p_x, p_y);
    y_tri();
    yr_tri();

    r_tri();
    rr_tri();

    b_tri();
    br_tri();
    popMatrix();
  }
  //黄色ひし形の三角形
  void y_tri() {
    vec_y[0] = new PVector(0, -r);
    vec_y[1] = new PVector(r*cos(5*PI/6), -r*sin(5*PI/6));
    vec_y[2] = new PVector(0, 0);

    PVector[] dir_y = new PVector[3];
    PVector[] next_y = new PVector[3];
    for (int i = 0; i < 3; i++) {
      dir_y[i] = PVector.sub(vec_y[(i+1)%3], vec_y[i]);
      dir_y[i].mult(0.5);
      next_y[i] = PVector.add(vec_y[i], dir_y[i]);
    }

    beginShape();
    fill(getCol0());
    stroke(getCol0());
    vertex(vec_y[0].x, vec_y[0].y);
    vertex(next_y[0].x, next_y[0].y);
    vertex(next_y[2].x, next_y[2].y);
    endShape(CLOSE);

    beginShape();
    fill(getCol1());
    stroke(getCol1());
    vertex(next_y[0].x, next_y[0].y);
    vertex(vec_y[1].x, vec_y[1].y);
    vertex(next_y[1].x, next_y[1].y);
    endShape(CLOSE);

    beginShape();
    fill(getCol2());
    stroke(getCol2());
    vertex(next_y[0].x, next_y[0].y);
    vertex(next_y[1].x, next_y[1].y);
    vertex(vec_y[2].x, vec_y[2].y);
    vertex(next_y[2].x, next_y[2].y);
    endShape(CLOSE);
  }
  //赤ひし形の三角形
  void r_tri() {
    vec_r[0] = new PVector(0, 0);
    vec_r[1] = new PVector(r*cos(5*PI/6), -r*sin(5*PI/6));
    vec_r[2] = new PVector(r*cos(5*PI/6), r*sin(5*PI/6));

    PVector[] dir_r = new PVector[3];
    PVector[] next_r = new PVector[3];
    for (int i = 0; i < 3; i++) {
      dir_r[i] = PVector.sub(vec_r[(i+1)%3], vec_r[i]);
      dir_r[i].mult(0.5);
      next_r[i] = PVector.add(vec_r[i], dir_r[i]);
    }

    beginShape();
    fill(getCol0());
    stroke(getCol0());
    vertex(vec_r[0].x, vec_r[0].y);
    vertex(next_r[0].x, next_r[0].y);
    vertex(next_r[1].x, next_r[1].y);
    vertex(next_r[2].x, next_r[2].y);
    endShape(CLOSE);

    beginShape();
    fill(getCol1());
    stroke(getCol1());
    vertex(next_r[0].x, next_r[0].y);
    vertex(vec_r[1].x, vec_r[1].y);
    vertex(next_r[1].x, next_r[1].y);
    endShape(CLOSE);

    beginShape();
    fill(getCol2());
    stroke(getCol2());
    vertex(next_r[1].x, next_r[1].y);
    vertex(vec_r[2].x, vec_r[2].y);
    vertex(next_r[2].x, next_r[2].y);
    endShape(CLOSE);
  }
  //青ひし形の三角形
  void b_tri() {
    vec_b[0] = new PVector(0, 0);
    vec_b[1] = new PVector(r*cos(5*PI/6), r*sin(5*PI/6));
    vec_b[2] = new PVector(0, r);

    PVector[] dir_b = new PVector[3];
    PVector[] next_b = new PVector[3];
    for (int i = 0; i < 3; i++) {
      dir_b[i] = PVector.sub(vec_b[(i+1)%3], vec_b[i]);
      dir_b[i].mult(0.5);
      next_b[i] = PVector.add(vec_b[i], dir_b[i]);
    }

    beginShape();
    fill(getCol1());
    stroke(getCol1());
    vertex(vec_b[0].x, vec_b[0].y);
    vertex(next_b[0].x, next_b[0].y);
    vertex(next_b[1].x, next_b[1].y);
    vertex(next_b[2].x, next_b[2].y);
    endShape(CLOSE);

    beginShape();
    fill(getCol2());
    stroke(getCol2());
    vertex(next_b[0].x, next_b[0].y);
    vertex(vec_b[1].x, vec_b[1].y);
    vertex(next_b[1].x, next_b[1].y);
    endShape(CLOSE);

    beginShape();
    fill(getCol0());
    stroke(getCol0());
    vertex(next_b[1].x, next_b[1].y);
    vertex(vec_b[2].x, vec_b[2].y);
    vertex(next_b[2].x, next_b[2].y);
    endShape(CLOSE);
  }
//反転
  void yr_tri() {
    pushMatrix();
    rotate(PI);
    y_tri();
    popMatrix();
  }
  void rr_tri() {
    pushMatrix();
    rotate(PI);
    r_tri();
    popMatrix();
  }
  void br_tri() {
    pushMatrix();
    rotate(PI);
    b_tri();
    popMatrix();
  }
}

int[] colors = {#bf0603, #083d77, #ff9f1c, #15616d}; //赤、青、黄色、背景
int getCol0() {
  return colors[0];
}
int getCol1() {
  return colors[1];
}
int getCol2() {
  return colors[2];
}
int getCol3() {
  return colors[3];
}