はじめに
Processingで歯車を作るために、曲線を理解したいと思い前回まではサイクロイド曲線をやってきました。
今回は歯車の形状に使われるインボリュート曲線を作りたいと思います。
インボリュート曲線とは?
インボリュート曲線とは、法線が常に一つの基礎円に接するような平面曲線です。
基礎円に巻かれた糸をたるまないように引っ張りながらほどくときに、糸の端点を描く曲線がインボリュート曲線になります。
Processingで動かすために糸の先端の座標点P\((x,y)\)を求めましょう。
点P\((x,y)\)の位置を求める
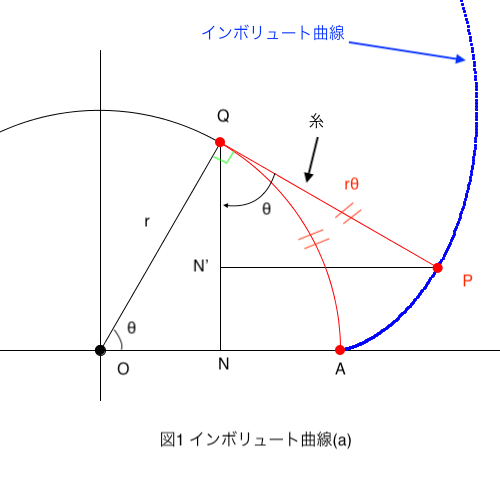
糸と基礎円の接点をQ、\(\angle{AOQ}=\theta\)とします。
PQは接線なので、
\[PQ\perp OQ \rightarrow \angle{PQN}=\angle{QON}=\theta\]
このとき、Pのx座標は
\[x=ON+N’P=r\cos\theta+r\theta\sin\theta\]
Pのy座標は
\[y=QN-QN’=r\sin\theta-r\theta\cos\theta\]
したがって、点Pのx座標とy座標をまとめると以下になります。
\begin{cases}
\large x=r(cos\theta+\theta\sin\theta) \\
\large y=r(\sin\theta-\theta\cos\theta)
\end{cases}
インボリュート関数を用いて点P\((x,y)\)の位置を求める
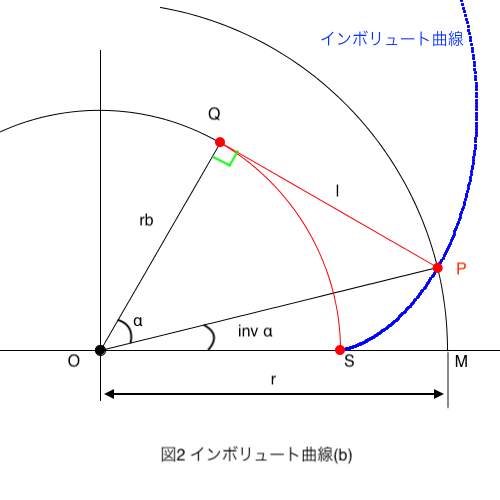
今回使うのは先程の上の式ですが、ここで歯車作成に使うインボリュート関数で 点P\((x,y)\)の座標を求めてみましょう。
ここで、\(\angle\)QOP=\(\alpha\,\),\(\angle\)POM=\(inv\,\alpha\)とします。OQ=\(r_b\,\),OP=rなので、角度\(\alpha\)は
\[\alpha=\cos^{-1}\frac{r_b}{r}\]
また、\(l=r_b\tan\alpha=\,\stackrel{\frown}{SQ}\,=r_b(\alpha+inv\,\alpha)\)より
\[inv\,\alpha=\tan\alpha-\alpha\]
したがって、点Pのx座標とy座標は
\begin{cases}
\large x=r\cos(inv\,\alpha) \\
\large y=r\sin(inv\,\alpha)
\end{cases}
それでは、Processingで動かしてみましょう。
Processingでインボリュート曲線
以下がProcessingでインボリュート曲線を動かすコードになります。
PGraphics pg1;
float x, y;
float theta = 0;
float r = 20; //基礎円
boolean Inv = false;
void setup() {
size(700, 500);
pg1 = createGraphics(width, height);
}
void draw() {
background(230);
//基礎円
ellipse(width/2, 220, r*2, r*2);
if (Inv) Involute();
}
void keyPressed() {
if (key == '1') {
Inv = !Inv;
theta = 0;
}
}
void Involute() {
//角度をラジアンへ変換
float rad = theta/180.0 * PI;
//インボリュート曲線
x = width/2 + r*(cos(rad) + rad*sin(rad));
y = -220 + r*(sin(rad) - rad*cos(rad));
//糸
stroke(0);
line(width/2+r*cos(rad),220-r*sin(rad),x, -y);
pg1.beginDraw();
pg1.noStroke();
pg1.fill(209, 0, 0);
pg1.ellipse(x, -y, 2, 2);
pg1.endDraw();
image(pg1, 0, 0);
if (theta >= 720) {
delay(3000); //2周したら3秒停止
Inv = !Inv;
}
theta++;
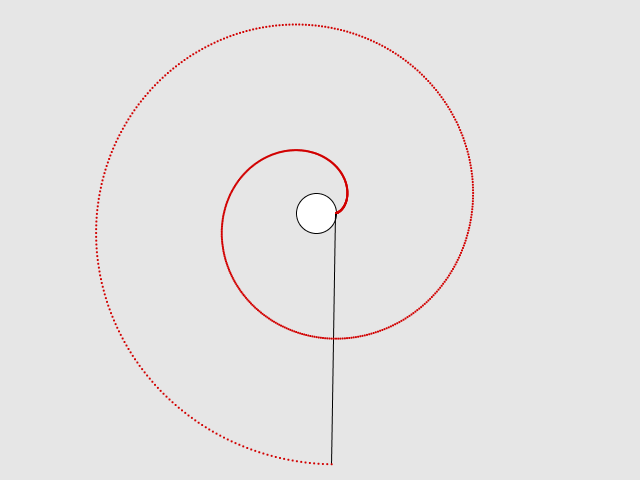
}アニメーション
実際の動作は以下のようになります。
参考文献
・Wikipedia-インボリュート曲線
https://ja.wikipedia.org/wiki/インボリュート曲線
・実用メカニズム事典
関連記事


コメント