はじめに
今回はProcessingでフーリエ級数を可視化したいと思います。
例として矩形波とノコギリ波を可視化します。
フーリエ級数とは
フーリエ級数とはwikiによると、複雑な周期関数や周期信号を単純な形の周期性をもつ関数の無限の和で表したものと書いてあります。
つまり、任意の曲線は正弦波と余弦波を無限に足し合わすと表現できると言い換えることができます。
言葉だけだと理解できないので式を見ていきましょう。
フーリエ級数展開の式
関数f(x)を周期2πの周期関数とし、以下のように三角関数で表すことをフーリエ級数展開といいます。
\[f(x)=\frac{a_{0}}{2}+\sum_{n=1}^\infty (a_n \cos nx+b_n \sin nx)\]
ここで周期関数f(x)は区画[0 , 2π]で定義されているとすると、フーリエ係数 \(a_0\) , \(a_n\) , \(b_n\)は以下の式になります。
\[a_0 = \frac{1}{\pi}\int_{0}^{\pi} f(x) dx\]
\[a_n = \frac{1}{\pi}\int_{0}^{\pi} f(x) \cos nx dx\]
\[b_n = \frac{1}{\pi}\int_{0}^{\pi} f(x) \sin nx dx\]
それでは、矩形波とノコギリ波のフーリエ級数を見ていきましょう。
矩形波のフーリエ級数
矩形波は、奇関数なので\(a_0\) = \(a_n\) = 0になり、\(b_n\)だけになります。
詳細は省略してf(x)は以下の式になります。
\[f(x)=\frac{4}{\pi}\sin x + \frac{4}{3\pi}\sin 3x + \frac{4}{5\pi}\sin 5x + \cdots\]
ノコギリ波のフーリエ級数
ノコギリ波も、奇関数なので\(a_0\) = \(a_n\) = 0になり、\(b_n\)だけになります。
詳細は省略してf(x)は以下の式になります。
\[f(x)=2(\sin x – \frac{1}{2}\sin 2x + \frac{1}{3}\sin 3x -\frac{1}{4}\sin4x + \cdots)\]
プログラム
以下は、Processingで可視化する矩形波のフーリエ級数のプログラムになります。
ControlP5で作成したスライダーを動かすことで、足す数を増やすことができ、より矩形波に近い形になります。
import controlP5.*;
float t = 0;
FloatList wave = new FloatList();
ControlP5 cp5;
int n;
void setup() {
size(600, 400);
cp5 = new ControlP5(this);
cp5.addSlider("n")
.setRange(1, 100)
.setValue(1)
.setPosition(250, 350)
.setSize(100, 20);
}
void draw() {
background(24, 48, 91);
pushMatrix();
translate(150, 200);
float x = 0;
float y = 0;
for (int i = 0; i < n; i++) {
float prevx = x;
float prevy = y;
float m = i * 2 + 1; //mは奇数
float r = 65 * (4 / (m * PI));
x += r * cos(m * t);
y += r * sin(m * t);
stroke(237, 247, 251);
noFill();
ellipse(prevx, prevy, r * 2, r * 2);
stroke(237, 247, 251);
line(prevx, prevy, x, y);
}
wave.insert(0, y); //波の方向を変えるために常に配列の先頭に追加する
translate(150, 0);
stroke(231, 49, 41);
line(x - 150, y, 0, wave.get(0));
beginShape();
noFill();
for (int i = 0; i < wave.size(); i++) {
vertex(i, wave.get(i));
}
endShape();
t += 0.02;
//300を超えたら配列の中の要素を削除する
if (wave.size() > 300) {
for (int n = 300; n < wave.size(); n++) {
wave.remove(n);
}
}
popMatrix();
}ノコギリ波の場合は、32,33行を以下に変更したらノコギリ波になります。
//ノコギリ波の場合
float m = i + 1;
float r = 70 * pow(-1, m+1) * (2 / (m*PI));動作確認
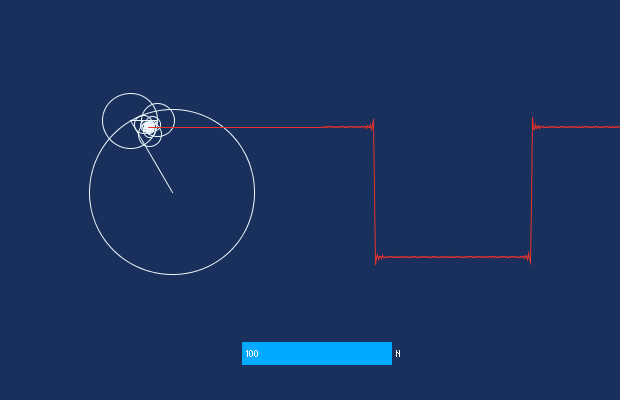
・こちらは矩形波の動作です。
・こちらはノコギリ波の動作です。
まとめ
今回はProcessingでフーリエ級数の可視化をしました。
式だけでは理解できなかったですが、可視化をしたことでフーリエ級数の効果を実感することができました。
次回は、フーリエ変換をやりたいと思います。
参考文献
・フーリエ級数-wikipedia
https://ja.wikipedia.org/wiki/フーリエ級数
・Processingをはじめよう
関連記事



コメント