Processingでハート形カムを作る

はじめに

今回は、Processingでカム機構を作りたいと思います。
カム機構でも種類がありますが、フォロワが等速度運動をするハート形カムを作成しProcessingで動作と変位を実装してみましょう。

ハート形カムとは？

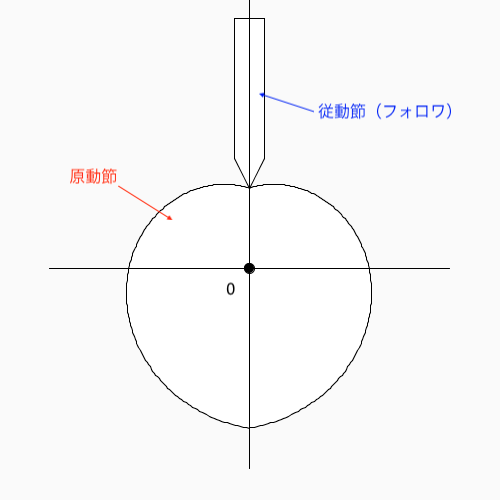
上図のように0を中心に原動節を回転させると従動節（フォロワ）は上下方向に動きます。このことから、回転運動を直線運動にする機構であることが分かります。

カムの形がハート形なので、ハート形カムと呼ばれます。

また、ハート形カムではフォロワが上下に等速度運動します。

ハート形カムの作成

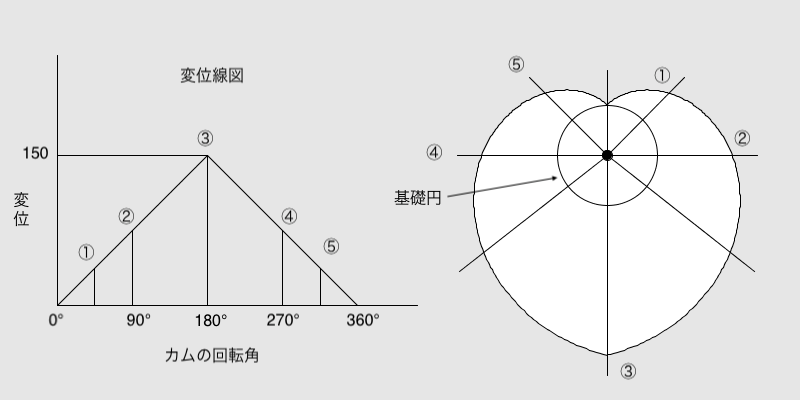
今回は、基礎円半径をr=50、変位をh=150としてハート形カムを作成します。

ハート形カムは、カムが1/2回転するまではフォロワは等速度で変位150まで上昇し、残りの1/2回転は等速度で下降するので上図の変位線図になります。

ハート形カムの形状を描く座標は、0°から180°までは次式で得られます。

\begin{eqnarray*}
x & = & (r+f(\theta))\sin\theta \\
y & = & (r+f(\theta))\cos\theta
\end{eqnarray*}

ここで、\(f(\theta)\)は傾きになります。
また、180°から360°の形状は反転させればいいだけです。

これをProcessingで書くと以下のようになります。

float r = 50; //基礎円
float h = 150; //変位
float f = h / PI; //傾き
beginShape();
for (float i = 0; i < PI; i += PI/180) {
    vertex((r+f*i)*sin(i), -(r+f*i)*cos(i));
}
for (float j = PI; j > 0; j -= PI/180) {
    vertex(-(r+f*j)*sin(j), -(r+f*j)*cos(j));
}
endShape(CLOSE);

アニメーション

以下は、ハート形カムのアニメーションです。変位線図が直線になっているのでフォロワが等速度運動しているのが分かると思います。

Processingでハート形カム機構 #Processing
ハート形カムでは、右の変位線図を見ると直線になっているで、加速度0よりフォロワが上下に等速度運動する。 pic.twitter.com/4g9NsYfFpI
— かめのの (@kameno_no3) December 12, 2020

Processingでハート形カムを作成するコード

以下はProcessingでハート形カムを作成するコードとなります。今回もクラスを使い実装しました。

スペースキーを押すとカムが回転します。

まずはメインタブです。

Heart_Cam cam;
Follower foll;
Graph graph;
boolean roll = false;

float r = 50; //基礎円
float h = 150; //変位
float f = h/PI; //傾き

void setup() {
  size(700, 600);
  background(230);
  cam = new Heart_Cam();
  foll = new Follower();
  graph = new Graph();
}

void draw() {
  background(230);
  translate(220, height/2+100);
  if (roll) {
    cam.update();
    foll.update();
    graph.update();
  } else {
    cam.display();
    foll.display1();
    graph.display1();
  }
  fill(250);
  ellipse(0, 0, 10, 10);
}

void keyPressed() {
  if (key==' ') roll = !roll;
}

ハート形カムのクラスです。

class Heart_Cam {
  float angle = 0;
  
  void display() {
    fill(255, 0, 0);
    beginShape();
    for (float i = 0; i < PI; i += PI/180) {
      vertex((r+f*i)*sin(i), -(r+f*i)*cos(i));
    }
    for (float j = PI; j > 0; j -= PI/180) {
      vertex(-(r+f*j)*sin(j), -(r+f*j)*cos(j));
    }
    endShape(CLOSE);
  }
  
  void update() {
    pushMatrix();
    rotate(angle);
    display();
    popMatrix();
    angle += PI/100;
  }
}

フォロワのクラスです。

class Follower {
  float x = 15;
  float y1 = 50;
  float y2 = 150; //フォロワ高さ
  float angle = 0;
  
  void display1() {
    float a = f * angle; //フォロワ変位
    fill(0, 0, 250);
    pushMatrix();
    translate(0, -r);
    beginShape();
    vertex(0, -a);
    vertex(x, -y1-a);
    vertex(x, -(y1+y2)-a);
    vertex(-x, -(y1+y2)-a);
    vertex(-x, -y1-a);
    endShape(CLOSE);
    popMatrix();
  }
  
  void display2() {
    float a = f * angle; //フォロワ変位
    fill(0, 0, 250);
    pushMatrix();
    translate(0, -r-2*h);
    beginShape();
    vertex(0, a);
    vertex(x, -y1+a);
    vertex(x, -(y1+y2)+a);
    vertex(-x, -(y1+y2)+a);
    vertex(-x, -y1+a);
    endShape(CLOSE);
    popMatrix();
    
  }
  
  void update() {
    if (angle < PI) display1();
    if (angle > PI) display2();
    if (angle > 2*PI) angle = 0;
    angle += PI/100;
  }
}

以下は変位線図を描くコードです。

class Graph {
  float angle = 0;
  
  void display1() {
    float a = f * angle;
    pushMatrix();
    translate(250, 50);
    line(0, 0, 220, 0);
    line(0, 0, 0, -200);
    ellipse(angle*30, -a, 10, 10);
    popMatrix();
  }
  
  void display2() {
    float a = f * angle;
    pushMatrix();
    translate(250, 50);
    line(0, 0, 220, 0);
    line(0, 0, 0, -200);
    ellipse(angle*30, -2*h+a, 10, 10);
    popMatrix();
  }
  
  void update() {
    if (angle < PI) display1();
    if (angle > PI) display2();
    if (angle > 2*PI) angle = 0;
    angle += PI/100;
  }
}